Relativity
– What I most admire about your art is your universality. You don’t say a word, yet the world understands you!
– True. But your glory is even greater! The whole world admires you, even though they don’t understand a word of what you say.
From conversation between Einstein and Chaplin
Relativity – a scientific theory that explains how our world works on a macro-level, combining mechanics, electrodynamics and gravity. Introduced by racial German Yid Albert «E=mc²» Einstein by compiling works of Dutch Lorentz, racial Yid Minkowski, Frogeater Poincare and his own of course. Divided into two parts: special relativity and general relativity.
History of the subject
At the turn of the 20th century increasing melancholy had been spreading amongst the physicist community. The students were advised by their professors against a career in physics in favor of law, since most of the laws have already been discovered and in 20-30 years, after the last nuances are figured out, there will be nothing left to do. All physics departments will be closed and the faculty given mops to clean the floors in law schools. It is described in Max Planck’s biography.

One of those not yet figured out nuances was how to marry Newton’s mechanics with Maxwell's equations (electrodynamics).
The source of the problem
“If the facts don't fit the theory, change the facts.”
Einstein quotes Hegel and Kant
Suddenly a discord was discovered between two physical studies: time-tested Newton’s mechanics and relatively young electrodynamics (which, amongst other things, describes propagation of electromagnetic waves). This propagation was described using Maxwell's equations, which were also tested by experiments and didn’t raise any doubt. It has already been established that light is also an electromagnetic wave and therefore the speed of electromagnetic wave propagation is equal to the speed of light. But an attempt to place a flashlight on a moving train and measure the speed with which the light from this flashlight travels ended in an epic fail and cognitive dissonance. In Newtonian mechanics the speeds of train and light should have been added together, but Maxwell's equations wouldn’t allow such a trick, and all the attempts to modify them to fix this problem failed. For example, if you fly after the light with its speed – speed of light, – this light according to Maxwell's equations… disappears. It would be as if there was no light at all.
Ether is the perfect drug for electrodynamics
Maxwell's equations, describing light propagation, were wave equations. A change in electric field creates a change in magnetic field, and a change in magnetic field creates a change in electric field – a wave spreads. If you fly after this wave at its speed a strange situation develops – the fields don’t change in space from the point of view of the observer, instead the fields are just motionlessly hanging in space not supported by anything, which is impossible to simulate in an experiment. Also, for a wave to propagate there needs to be a medium which will conduct the oscillation. To conduct an acoustic wave (sound), for example, there needs to be air. Well, what if the electromagnetic wave also propagates in some kind of specific medium? This magical substance was named ether. Ether was one of the models used to try and explain first electrodynamics, then later – gravity, Mendeleev even tried to use it to explain the Periodic Law.
In the simplest models ether and matter were different entities and the former didn’t physically resist the latter. But this approach created problems of its own: if ether was ideal liquid and particles - ideal balls, then friction forces responsible for the creation of magnetic field would disappear, otherwise there would be dragging of particles against ether. The magnetic field was being observed, which led to a conclusion: since ether exists on its own, then we should be rubbing against it when flying through it together with the Earth. But since this rubbing wasn’t being observed – ether had to be attributed with magical properties – ether had to be simultaneously absolutely dense for conducting electromagnetic waves, and absolutely sparse to avoid energy losses.
Also, according to the ether-based interpretation, since the Earth moves through ether, all the light on it should get “blown away by adverse ether wind”. Scientifically it was called “light speed anisotropy” and the scientists were really determined to find this “wind”. In the end Michelson and Morley conducted an experiment but didn’t find the sought-for effect. Technically, they measured something but six times weaker and in the wrong direction. The scientific community began to contemplate how to live with this knowledge. And all that was left from the ether-theory were notions like “field strength” and “current” in electrodynamics.
Einstein
Nature and nature’s laws lay hid in night:
God said, Let Newton be! and all was light.
It did not last: the Devil howling “Ho!
Let Einstein be!” restored the status quo.
First two lines – Alexander Pope (1688—1744)
Second two – J.C. Squire (1884—1958)
The physicists had to start all over. The most successful turned out to be the aforementioned Lorentz, whose equations tried to explain the failure to discover ether by presuming that movement of matter through ether caused such changes in matter itself, that made the discovery of light speed anisotropy impossible, and Poincare. The postulates of special relativity are largely based on their equations, even though they were designed based on different presumptions. Einstein, however, showing tremendous mental flexibility and fortitude, not giving up even where regular drugs weren’t effective enough, offered an alternative interpretation of the equations from an entirely different angle.
Commonly, the physicists prioritized Newtonian mechanics and attempted to tweak Maxwell’s equations to fit. But Einstein suggested the opposite: it's Maxwell's equations that are correct and Newtonian mechanics needs to be tweaked.
The mindfuck has begun.
Special relativity
Arthur Eddington was once asked by Ludwig Silberstein: “You must be one of three persons in the world who understands general relativity." On Eddington's demurring to this statement, Silberstein responded, "Don't be modest, Eddington," and Eddington replied, "On the contrary, I am trying to think who the third person is."
Famous anecdote
The postulates of special relativity
What does “Maxwell's equations that are correct” mean? It means that in any inertial frame of reference the laws of electrodynamics (and not just mechanics) are identical (invariant) and therefore the equations don’t change. From the transformation equations in transition between these inertial frames in turn can be seen, assuming the “equality” of all the points in the universe (homogeneous space) and all directions (isotropy), that the speed of light in all the frames is the same.
Small clarification: inertial frames of reference – are such frames of reference in which an isolated physical object with no force acting on it moves with constant velocity, in other words, such frames where Newton’s laws of motion hold. The postulates of special relativity are formulated for inertial frames, together with Newton’s laws. Einstein didn’t invent anything new here.
For those who missed the nuance: Galilean addition of speeds used in Newtonian dynamics went out the window. The beam of light radiated from a flashlight on a moving train will move with the same speed relative to the train itself and to a train station. Meaning it will fly away at lightspeed from a train station. And it will fly away at the same lightspeed from the train. And from the flashlight. And from the train. At the same speed. Even though they move relative to each other!!!
There are totally three postulates:
- Einstein’s principle of relativity: all physical laws are the same in every inertial frame of reference for any body moving at constant velocity as for any body at rest.
- There’s a finite (maximum) speed of propagation of force
- Space and time are homogeneous, space is also isotropic.
The first postulate might seem like it was stolen from Galileo, but back then it only applied to Newtonian mechanics, not all physical laws. Actually, there wasn’t anything else beside Newtonian mechanics at the time, so it would be more correct to call it “Galileo’s principle of relativity”, thankfully Einstein has plenty of his own merits. The really important one is the second postulate. Everything else comes out of it, including the impossibility of moving faster than the speed of light for a material object, and moving with the speed of light for a massive object (only slower).
The third postulate is used for solving the Lorentz transformation and already existed in Newtonian mechanics. The laws of conservation of momentum, energy and angular momentum are corollary from it.
If you take a piece of paper and a pencil and start schematically drawing the train experiment according to the second postulate, the result will be brutal nonsense. It turns out that the time of the same process calculated in the train’s frame of reference and train station’s frame of reference would be different. Time. Different. Completely. Time. For a moving and a stationary object. Different. Something doesn’t fit.
“Well, what if time really is different?” – Einstein asked himself, and damned if he wasn’t right. But how much acid he had to ingest to send his thoughts in that direction the history doesn’t tell (although the phrase “imagination is more important than knowledge”, attributed to Einstein, gives us a clue).
Relativity of simultaneity. Lorentz transformation
So, one of the important conclusions from this strange behavior of light, or to be more precise its speed, was that events simultaneous in one frame of reference wouldn’t be simultaneous in another frame of reference if these frames move relative to each other.
Any other scientist at this point would shred his work into pieces, but Einstein kept meticulously working the equations. The result was the equations for conversion of coordinates, both in space and time, from one frame of reference to another, which are now called Lorentz transformations. The thing is, Lorentz formulated these equations before Einstein, but used them to eliminate the contradictions between Newtonian mechanics and electrodynamics. It led to funny results: both space and time in different frames of reference look different if they move against each other. Also, space coordinates depended from time coordinates in the transformation equations, and the other way around. It created a space-time dependency, meaning time and space are inseparable and together form a single spacetime continuum.
The most known effects of Lorentz transformation are:
- Length contraction, or Lorentz contraction. If a rocket was flying by us, its length measured in our stationary FoR would be shorter measured along its velocity vector, than its length measured when the rocket is still, and the faster it flies by us the shorter the measurement will be. In the limiting case, if the rocket flew at the speed of light, its length would become zero.
- Time dilation. Time intervals between events would be longer from our point of view, than the same intervals measured from a moving rocket, and the closer its speed is to the speed of light, the longer the intervals. In the limiting case, if the rocket flew at the speed of light, it would seem to us that time stands still inside it.
If somebody thinks that from the rocket in case of these perturbations we would look elongated and with a fast running watch – this isn’t the case. Due to relativity of movement from the rocket's perspective (it was flying with no acceleration in a linear motion) it was actually still, while we were flying by, and an observer inside it would see us shortened (narrower) and with a slow running watch.
These effects are commonly known but don’t give the full picture. The full picture are the Lorentz transformations themselves. Any attempt to view special relativity only through these effects usually leads to paradoxes. That’s where most of the special relativity critic’s fail.
Speed of light and causality
Another corollary of Lorentz transformations is that moving faster than the speed of light would cause time intervals to be measured in imaginary numbers, which doesn’t have any physical meaning in Newtonian mechanics. Even Einstein’s twisted brain couldn’t handle that, so it was decided: it is impossible to move faster than light in vacuum. Special relativity prohibits an object with mass to reach the speed of light. And causality prohibits tachyons (particles that hypothetically travel faster than light) to interact with pre-lightspeed objects.
So the speed of light in vacuum became not only invariant (equal for the same beam of light in all frames of reference), but also the maximum possible speed for anything at all. In Einstein’s mechanics it corresponds to the fact that accelerating a massive object to the speed of light would require an infinite amount of energy, which is obviously impossible.
It is possible to move faster than light in a certain medium, Pedowikia knows. But the light moves slower than the speed of light in vacuum there, so everything is tip-top.
E=mc²
The ancient as the world itself equation, in classical mechanics – direct result of Meshcherskiy’s equation for a body radiating particles at the speed of light. First formulated by Oliver Heaviside (1889), then Samuel Tolver Preston (1895), Kelvin (1903), Olinto De Pretto (1903), Henri Poincare (1904), Friedrich Hasenohrl (1904), Max Planck (1907).
Equations of classical mechanics had to be reformulated in accordance with relativity. One of these equations was the equation for kinetic energy of an object. For those who forgot school-level physics: the kinetic energy of a flying piece of mass is the amount of work needed to accelerate this mass from a state of rest to its current speed. And work is the product of distance, force and cosine of force application and direction of travel, integrate, differentiate and Ta Da, Newton got the well-known em-vee-squared-by-half (Ek=mv²/2).
Einstein, however, instead of integrating and differentiating, expressed it in power series of “v” and as a result got that relativistic kinetic energy is the difference between a term that depends on speed (and becomes zero at rest) and a term that doesn’t depend on speed and is always equal to mc². It should be obvious by now, that something as small as a term in some equation wouldn’t stop Einstein, so a conclusion followed: even for a body to be at rest requires an amount of energy equal to E0=mc², and full energy E=Ek+E0. Suddenly the relativistic equation for impulse collapsed from a multi-storied mathematical apparatus into a single elegant equation.
This way a concept of mass–energy equivalence was born, perfectly proven in nuclear physics. In every mass, even at rest, there’s a fuckton of potential energy – Hiroshima can attest to that. Einstein himself, by the way, was very displeased when he learned how the generals used his discoveries. According to pop literature, that’s when he started going bonkers.
To transform the entire mass into energy is only possible by annihilating it with the same amount of antimatter. Unfortunately, creating antimatter is a very laborious activity.
Not only does the equation reveal the correlation between mass and energy, what’s also interesting is the theoretically resulting coefficient c², which makes the equation look so graceful, since it unites two seemingly unrelated hypostases – matter and field. Thinking technically, what do matter (mass) and light (electromagnetic wave) have to do with each other.
As a matter of fact, during movement E=γmc², where γ=1/(1-v²/c²)^0,5, m —rest mass. Therefore, if v<<c E=γmc²=mc² + mv²/2 + … (following are negligently small compared to mv²/2 terms), so at relatively small speeds general relativity comes to Newtonian mechanics.
Minkowski space
A large contribution to SR was later made by a mathematician Hermann Minkowski. He showed that Lorentz transformations work well on graphs, if these graphs represent pseudo-Euclidean space with signature (3,1). Sounds complicated, and very well is. All it means is that we live not in Euclidean space, but in Minkowski’s pseudo-Euclidean spacetime, also called light cone. Not every school will teach you that. ZOG tries to hide it, but physicists know.
In Minkowski space lies the essence of modern (last hundred years) interpretation of SR. Roughly speaking, our spacetime is 4-dimensional. Add to that the fact that it is not common (Euclidean) 4d space, but instead pseudo-Euclidean spacetime with aforementioned metrics. It means that in this spacetime the distances are measured a little differently. For example, the twin paradox boils down to the fact that the twins flew in this spacetime different distances, called “intervals”, leaving from one spot (place in space and moment in time) and meeting in another (it doesn’t matter that it’s the same place in space, the moment in time is different), in a same way as two cars that travel by different roads used different amounts of gas, even though they met in the same place.
To put it even simpler: when we speak of relativistic 4d spacetime, we don’t mean any special fourth dimension (like curled up dimensions in string theory) and the underworld inside it. The revolutionary aspect is that there is no absolute time separate from the frame of reference and 3d space, in the same way as there’s no absolute space with a spherical coordinate system and absolute distances. Space and time, separated in a regular jackoff’s mind more than apples and oranges, become part of a single continuum that contains all the physical processes in the universe.
General relativity only alters this picture to a degree that this Minkowski spacetime is also curved.
General relativity
A problem again
After developing SR and perfectly explaining basic mechanics and electrodynamics within its limits, Einstein was once again faced with a question: “WTF?”. Only this time the “F” was gravity. SR decidedly refused to marry with gravitational forces. To solve the problem Einstein had to rape his brain for seven years and develop an extremely complicated theory of gravity, named General relativity. It hides under the following spell:
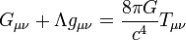
The core of the problem
According to Newton, gravity was described as force field interaction: any objects with mass creates a gravitational force field around it which attracts other objects with mass. The important point here is that gravity is force. This is where light started fucking with physisits again. See, light is an electromagnetic wave, i.e. field structure, not possessing mass, meaning that according to Newton gravitational force shouldn’t affect it: no mass – no force, that could act upon it. But if gravitation force doesn’t act upon light, then the conservation laws go out the window.
“When is this shit going to end?”, – cried out Einstein and started drthinking again.
Gravity is such gravity
“Gravity is a pretty weird thing” – Einstein finally realized. And there were good reasons to think that. Since ancient times scientists have been haunted by a question: why is gravitational mass the same as inertial? Galileo, for example, timed two different sized balls rolling down a slope, and both times were the same within the margin of error. It turns out that objects with different masses fall down in the gravitational field with exactly the same acceleration. Newton accounted for that fact by adding mass to the gravitational force equation, and when it comes to calculating the travel of an object in a gravitational field, its mass is simply reduced in numerator and denominator and doesn’t affect the result. It means that it doesn’t matter what the masses of falling objects are, if starting conditions are the same then they will move absolutely identically.
“It doesn’t quite look like a normal force, – thought Einstein. – The bigger the mass the less effect the force should normally have. By its definition. Something’s not right here!” Inflamed by brilliance, the brain made another mind bending backflip and asked itself the epic question, which led to everything that follows: “Is it even force?”
The elevator experiment
How do we know that there’s force acting upon us? It is actually easy to establish: when we sit in an accelerating car we feel how we get pushed into the seat. Once we accelerate and begin to travel with constant speed - we don’t feel it anymore. If we were moving on ideally even surface we wouldn’t feel any difference at all from sitting still. The fact that there’s no difference is reflected in the equality of all inertial frames of reference: during uniform linear motion all processes and laws are identical: it’s impossible to experimentally tell one FoR from another. What would we feel if we were placed inside inertial FoR – we would feel weightlessness, we wouldn’t be pulled in any direction, just hang there in one spot and that’s it.
“It is so strange – thought Einstein, – that if you place a man inside a free-falling elevator he would feel weightlessness. Meaning, he wouldn’t be able to tell without looking outside whether he is free-falling in the gravitational field or just steady floating (moving uniformly and linearly) in outer space far from all gravitating masses.” Another strange thing is that if we were to fixate the elevator in the gravitational field (stop it on some floor), the man inside it would feel acceleration acting on him. If he were conducting experiments inside this stopped elevator the results would be the same as if he was accelerating in outer space: he would be pressed into the floor by some force like in an accelerating car.
“But if it is impossible to experimentally tell a free-falling in gravitational field frame of reference from moving uniformly and linearly (inertial), then maybe it actually is moving uniformly and linearly (is inertial)?” – Einstein cleverly asked himself, and once again was right.
Spacetime curvature
A regular jackoff at this point would say: “Hold your horses! An object free-falling in a gravitational field can’t move uniformly and linearly. It is easy to prove – just throw a rock at an angle to the ground: its trajectory would be far from linear and its movement far from uniform, it is obvious!”. Einstein couldn’t give two fucks what was obvious to whom and what makes sense to regular jackoffs. Since no instrument inside an object can tell free-falling from uniform linear motion, then it is uniform and linear. But then why do we see the parabolic trajectory of a thrown object?
It is unknown whether the concept was borrowed by Einstein from Riemann, who creatively expanded Lobachevsky, or he got there himself and only used already available math, but what is known is that the mathematical apparatus of the subject was developed by Riemann and Lobachevsky long before Einstein. The flying rock miracle can be explained by the fact that it’s not the trajectory of a rock that is curved, but the spacetime itself, through which it moves. This spacetime is called Riemannian spacetime and is a much more brutal thing than Minkowski’s spacetime. It is worth mentioning, that when the orderlies from the local nut-house started worrying about Einstein’s mental health, he was able to disprove a suspicion of psychosis by referencing Lobachevsky’s geometry and explaining to the psychiatrist, that it’s common amongst physicists to spew such nonsense and no Haldol was needed.
What does “curved” mean?

Vague analogy.
Two ants are crawling on the surface of an apple. Each one uniformly moves forward without turning. They started at the same spot, moving in the opposite direction. After a while to their surprise they will find themselves in the same spot again, even though they moved in the opposite direction linearly and uniformly.
The rock’s trajectory is kind of the same deal: even though it parted with the surface of the Earth at the beginning of its path, and even though it was flying linearly and uniformly, just like Earth, eventually their paths crossed again in the curved 4d spacetime: the rock falls back on the ground.
Another vague analogy.
Take a rubber membrane (ideally very thin condom latex), stretch it parallel to the ground (I know). Put something heavy in the middle, like an orange. The membrane will sag. There’s your space curvature, a 2d space, but nonetheless. If we were to linearly and uniformly launch a ball on this membrane now, pre-coating it with paint, its trajectory will be a curve, not a straight line. We can even achieve a satellite effect when the ball will roll around the orange and will eventually fall on it (nobody canceled friction). And if we were to roll the ball from the orange at a tangent we will get our ballistic curve from the previous example.
This example also illustrates the ball’s own space curvature on the membrane, albeit much smaller than orange’s.
You can also simulate a binary star by rolling two large balls (oranges don’t roll too well) towards each other on parallel courses. If the initial speeds are correct, they will start rotating around a single “center of mass”. This example is another flat illustration of space curvature due to gravitational field.
To imagine this curvature in 3d, instead of a sagging membrane, think of a field, which has higher density closer to the ball and reduces with distance (think density instead of depth).
It’s worth mentioning that these analogies really are vague. In the condom analogy there are real physical forces acting on the rolling objects (normal force). In the apple analogy the 2d surface of the fruit is inserted into common 3d space, which can also lead to false conclusions. The curved space on the other hand isn’t inserted into anything and doesn’t act with any forces. It’s just that the shortest distance between two points in it isn’t necessarily straight, and translation of a segment along a closed curve doesn’t necessarily match the initial segment.
What curves space and time? According to GR it is curved by presence of mass (energy–momentum to be precise). Presence of mass acts in such a weird way on space, that distance between two points in space changes in time (also a vague analogy, since space and time are interdependent, like in SR, and saying “space changes in time” isn’t technically correct, it requires introducing a coordinate system and building isochronic sections – really easy to strain something in the head).
To summarize, a beam of light flying by a massive object:
- Doesn’t experience any force and flies uniformly and linearly.
- But the distance between it and a massive object changes due to the presence of spacetime curving mass, which makes it seem that the path of light deviates from a straight line.
Such perturbation elegantly solved the light in gravitational field problem, and explained why all objects fall with the same acceleration despite their mass. There simply is no falling, the spacetime is curved and the objects moving in it uniformly and linearly will move the same if the initial conditions are the same. Indeed, there’s no correlation between mass and uniform linear motion, and the fact that spacetime is curved – well, sorry, but nobody promised it would be easy.
Effects predicted by GR
- Gravitational deflection of light. In particular, the gravitational lensing effect appears when there’s a massive object between the source of light and the observer. As a result this object acts kind of like a lens, whose gravity deviates the path of electromagnetic wave. A well-known example – Einstein Cross. The light from quasar is split and deflected by a closer galaxy, and as a result we see four different images of the same shit.
- Gravitational redshift. Light’s frequency will decrease (its spectrum will shift towards the red end) when it travels out of a gravitational well (when it’s moving away from something rea-a-aly heavy). Was discovered in the spectrum of stars including the Sun and proven in some experiment.
- Geodetic effect. The axis of a spinning object (planet) spins itself, and not because there is some force acting on it, but due to the curved spacetime. Although precession of planets has been known since Kepler, it was explained by external forces changing the energy-momentum vector. But while its absolute value was calculated according to the Newtonian model, its results deviated from the real observations. GR equations however produce results that match the observations within the margin of error.
- Apsidal precession. Rotation of the planet’s orbit. Was calculated on paper by Einstein and matched the observed later precession of Mercury.
- Predicted the existence of gravitational waves. Until a certain moment there were only indirect evidence from reliable observations of binary start and double pulsars, like PSR J0737−3039 and PSR B1913+16. But in 2016 the megabrains from LIGO reported first direct observation of gravitational waves.
- Gravitational time delay (Shapiro effect). Electromagnetic wave travels longer close to a massive object, than if there was no object. The effect is confirmed.
- Gravitational time dilation. The closer a watch is to a massive object, the slower it ticks. The effect was confirmed in Pound–Rebka experiment and is accounted for by Global Positioning System.
- Black holes – a topic for a separate article.
Deniers
If something seems stupid, but works, then it isn’t stupid. You are simply too dumb to see that it’s actually clever.
Murphy's law
Einstein dies and goes to heaven:
– Albert, my son, you led a virtuous life. Is there anything you want to ask me?
– Please, God, show me the equation of everything!
Snap of the fingers, a whiteboard covered in equations appears. Einstein, while studying the equations:
– Newton already knew that, I knew this, this seems plausible… Oh, this I suspected. Hm. God, I think there’s an error here.
– I know…
General theory of relativity is first of all that, a theory, not ultimate truth and technical documentation for creation of the universe. This theory is partially confirmed by experiments and partially not. Based on experimental data some aspects of the theory get developed or modified. Right now, not a hundred years ago on its author’s desk.
Regular jackoffs even if they heard about theory of relativity consider it too complicated and boring, and therefore don’t criticize it, although Einstein’s racial yidishness causes some butthurt with antisemites.
College kids like to criticize special relativity. As a matter of fact, special relativity finds itself in the unique position amongst other products of scientific thought. It isn’t the only theory being “attacked”, but not many others are being attacked so often and ferociously. On one hand, it’s still simple enough in its expressions and equations to be understood by students. At the same time it already contradicts common sense so much that the revelations of “it’s obviously all bullshit” kind are almost guaranteed at the first introduction. Most of the time the critique boils down to a template: “All his stupid theories racial yid Einstein stole from his racial slavic-serb wife and racial dutch asshole Lorentz”. Aren’t capable of criticizing general relativity, since tensor calculus is beyond the skill level of these critics.
Office plankton on the rare occasions when it bumps into the affairs of the scientific community, usually experiences catatonic stupor from the attempt to comprehend the state of modern science. Many get unhappy though that Lucas lied in his saga not only about the sound of his tie-fighters in vacuum, but also about space travel in general.
According to SR, colonization of space is possible in principle, but it will look completely different than in Star Wars. The thing is, from Earth’s perspective, the spaceships that were launched from it will never reach speed of light, and it will take hundreds/thousands/millions/billions of years to reach their destination (closest to us galaxy, Sagittarius dwarf spheroidal galaxy, is 70 thousand light years away), depending where they go. But from the spaceship’s crew’s perspective they can reach farthest galaxies in the universe at reasonable time, depending on the capabilities of the engine they can reach the closest star in a matter of minutes (engines like that haven’t been invented yet of course), they just have to make sure the acceleration doesn't squash them, but that’s a technical issue. Because during acceleration the spaceship travels through a section of Minkowski spacetime where distance to the stars becomes much shorter (Lorentz contraction) and it won’t take long to cover it. As a result we have a following picture: it is possible to send a colonization ship in the furthermost corners of the galaxy, it will reach it without getting all raggedy, but we probably won’t ever hear back from it (it is colorfully described in the Consul's tale at the end of Dan Simmons’s “Hyperion” and also covered in detail in Poul Anderson’s “Tau Zero”). Of course there are other problems with space travel: outer space is absolutely stuffed with all sorts of high-energy radiation, fast electrons, interstellar gasses and malicious aliens. And if it’s already hard enough to maneuver between large objects in shortened (contracted) distances, it is impossible to out-maneuver radiation. So, at high speed and with decent length contraction even background relic radiation thanks to the Doppler effect turns into hellfire incinerating any material known to men. And a speck of dust at this speed turns into a nuclear bomb.
Most scientists got tired of arguing with criticizing public long time ago and simply redirect all attacks on Einstein’s theories to the same place as attacks on conservation laws – in the black anal chasm of torsion fields and other pseudoscience. Of course, the premises of relativity critique weren’t always the desire to preserve traditional materialism and determinism, a lot of the time it was due to its utter contradiction with intuitive perception of the world by majority of people, hence the perpetual desire to find a medium for the propagation of light waves – ether. By the way, Einstein also later suggested to return ether back into science, but for a different reason. He simply stated that it’s not right to call space, that has so many parameters, vacuum.
Special relativity wasn’t widely accepted right after it was published. Even Lorentz, who was teaching math special relativity was actually based on, didn’t agree with Einstein’s interpretation and believed in ether until the end of his life. The so-called paradoxes of SR were made up in the teens-twenties of the last century to troll the new theory, but were all resolved at about the same time. SR was denied/critiqued by many prominent scientists: Tesla, Lenard, Stark, Zhukovsky, J. J. Thomson.
Unlike special relativity (in terms of its applicability), general relativity has few open problems. It makes it more vulnerable to critique than SR, and even Einstein wasn’t happy about it, after finishing GR he tried to develop the so-called “Unified field theory”, that would describe absolutely everything, but failed.
The problem with the energy
There’s one small problem with GR: the energy isn’t being conserved, to be precise it is, but only after certain sorcery. The problem arises from the structure of Einstein’s equations:
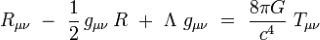
On the left we see curved space, i.e. gravitational field. On the right – energy-momentum, i.e. matter. The nuance is that there's no gravitational field on the right side, because it’s all on the left side. Meaning, all energy is pinched by matter and the gravitational field is left with empty pockets, though even high school students know (I hope) that there’s potential energy of gravitational field, on top of that it’s later found that gravitational waves transfer energy, even though they can’t. So, there’s this spinning double star, gravitational waves carry energy away from it, energy decreases, but energy flux is still zero, like nothing is happening.
Discord with QM
GR, unlike SR, contradicts another generally accepted theory – quantum mechanics, that describes the processes in the micro-world, more on the subject here.
Solution
An alternative to GR must satisfy very strict specifications – at speeds close to c and low gravity must come to SR; at high gravity must describe the effects of GR as well as GR; at low gravity and low speed must come to Newtonian mechanics. And it must predict something different from GR predictions, verifiable by experiment. Suddenly, there was a shitton of those theories. However, despite the simplicity of GR’s expression in tensors, it actually has some teeth-crushing math behind it, alternative theories – even more so, and there’s no free physicists, nor free oil to check all these theories for scientific validity and compliance with experimental data. So the mainstream of physics went another direction, two actually:
- Development of theories that can marry GR with QM and result in the theory of everything. String theory, for example. It has its own unresolved problems, but that’s a different story.
- Design of the experiments that can disprove GR. However, the effects are so small that the experiments require very big hundreds of money. Also, in 1998 they conducted an experiment that disproved GR – discovered accelerating expansion of the universe. And ironically this discovery fit GR better than the alternative theories, simply had to reintroduce a term with the cosmological constant that was first added by Einstein to stabilize the universe and later thrown out by Friedmann. Named it dark energy, nobody knows what the fuck it is, but the equations work.
As a result, GR remains a generally accepted theory, not because of blind faith in it, but simply because nobody offered anything better, and the experiments don’t contradict it to such an extent, that it’s better to move on to something different, than to fix what is. Of course there are still scientists who envy Einstein’s fame and continue inventing alternatives, but usually they don’t get a lot of funding to test their theories. One example would be MOND, although today nobody really takes it seriously anymore.